Entropia#
Fundamentos Teóricos#
Entropia é a função termodinâmica que aponta o sentido de uma transformação espontânea e é definida a partir de uma transformação reversível, onde
nesta equação \(dQ_{rev}\) é a quantidade calor trocado em uma transformação reversível. A entropia só depende do estado final e inicial do sistema. Logo, em uma transformação cíclica \( \Delta S = 0\).
A variação da entropia pode ser cálculada para diferentes transformações reversíveis:
Mudança de fase reversível a T e p constantes : \( dS = \frac{\Delta H}{T} \)
Aquecimento reversível a p constante sem mudança de fase : \( dS = \frac{Cp}{T} dT \)
Transformação reversível em função de T e V : \( dS = \frac{Cv}{T} dT + \frac{\alpha}{\kappa} dV \)
Transformação reversível em função de T e p : \( dS = \frac{Cp}{T} dT - \alpha V dp \)
Quando a transformação é irreversível, buscamos uma transformação reversível entre os mesmos estados final e inicial, de forma que as equações anteriores possam ser aplicadas. Todas as equações anteriores se referem ao sistema e não contem nenhum informação sobre as vizinhanças. No entanto, a relação entre espontaneidade de processos e entropia está associada a variação da entropia do sistema mais vizinhanças, chamada de entropia do universo ou entropia total. Esta pode ser descrita pela equação
Em um processo reversível \( \Delta S_{universo} = 0 \). Apesar de \(\Delta S_{viz}\) e \( \Delta S_{sis} \) variarem, a entropia do universo se mantem constante em processos reversíveis. No caso de processos irreversíveis
\( \Delta S_{universo} > 0 \)
Por consequência, a entropia deve aumentar em transformações espontâneas. Enquanto que \( \Delta S_{universo} = 0 \) define um estado de equilíbrio.
Os seguintes módulos precisam ser carregados para resolução dos exercícios:
# Tudo começa com a importação dos módulos necessários para fazer as contas
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
from scipy.integrate import quad
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 2
1 # Tudo começa com a importação dos módulos necessários para fazer as contas
----> 2 import numpy as np
3 from scipy.optimize import curve_fit
4 import matplotlib.pyplot as plt
ModuleNotFoundError: No module named 'numpy'
Exemplo 1: Obtendo o polinômio da capacidade calorífica#
A tabela abaixo apresenta os valores de \(Cº_{p,m} (J mol^{-1} K^{-1})\) para \(O_2(g)\) no intervalo de tempertaura de 298K até 1500K. a) Ajuste um polinômio de terceiro grau ao dados de capacidade calorífica em função da temperatura e construa o gráfico de \(Cº_{p,m}\) versus temperatura. b) Uma segunda alternativa é ajustar uma função do tipo \(Cº_{p,m} = A + BT + CT^2 + D/T^2 \) aos dados fornecidos. Ajuste esta função aos dados fornecidos e construa o gráfico de \(Cº_{p,m}\) versus temperatura. c) Compare os resultados obtidos.
T (K) |
298.15 |
400. |
500. |
600. |
700. |
800. |
Cp (J/K mol) |
29.376 |
30.106 |
31.091 |
32.090 |
32.981 |
33.733 |
T (K) |
900. |
1000. |
1100. |
1200. |
1300. |
1400. |
Cp (J/K mol) |
34.355 |
34.870 |
35.300 |
35.667 |
35.988 |
36.277 |
Solução#
Como os cálculos de variação da entropia dependem dos valores da capacidade calorífica, é importante conhecermos diferentes formas para expressar Cp(T). Os valores dados na tabela serão escritos na forma de vetores e em seguida as funções informadas no enunciado serão ajustadas aos dados.Incialmente será feito o ajusta a uma função polinomial de terceiro grau e em seguida a segunda função será ajustada.
T = np.array([298.15,400.,500.,600.,700.,800.,900.,1000.,1100.,1200.,1300.,1400.,1500.])
Cp = np.array([29.376, 30.106, 31.091, 32.090, 32.981, 33.733, 34.355, 34.870, 35.300, 35.667,35.988, 36.277, 36.544])
#Ajuste polinomial
deg = 3 #grau do polinômio
z = np.polyfit(T, Cp, deg) #objeto que guardará os coeficientes do polinômio
y = np.poly1d(z) #polinômio criado com os coeficientes ajustados
#Impressão dos resultados
print('Cºp,m = ' + format(z[3] , ' 6.5f') + ' +' + format(z[2] , ' 6.5f') + 'T' + format(z[1] , ' 6.5e') + 'T²' + format(z[0] , ' 6.5e') + 'T³')
#imprimir diretamente o polinômio:
print(y)
Cºp,m = 25.66508 + 0.01304T-3.81147e-06T²-5.57560e-11T³
3 2
-5.576e-11 x - 3.811e-06 x + 0.01304 x + 25.67
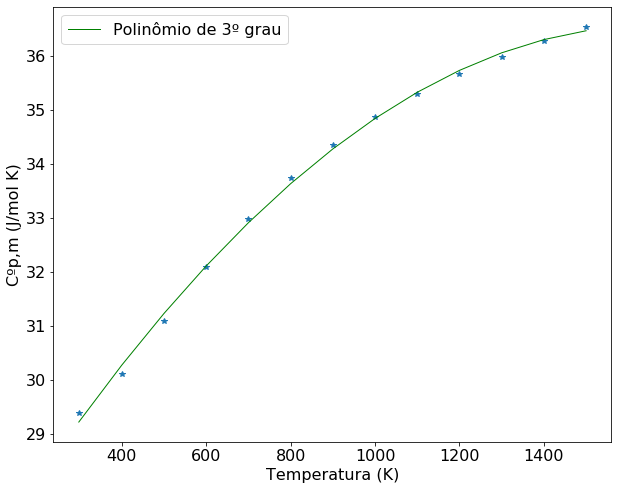
Foram mostrados os resultados de duas formas distintas para fins comparativos. A criação do polinômio y pode facilitar algumas operações, como a construção de gráficos. O gráfico de Cp versus T será construído usando o polinômio y, considerando os valores de temperatura informados no enunciado do problema.
plt.rcParams.update({'font.size': 16}) # estes dois parâmetros precisam aparecer antes da definição do plot
plt.figure(figsize=(10,8))
#plota os valores informados no enunciado na forma de pontos
plt.plot(T,Cp,'*')
#plota o polinômio ajustado como uma linha
plt.plot(T,y(T), color='green', linewidth=1, label='Polinômio de 3º grau')
#definição da legenda dos eixos
plt.xlabel('Temperatura (K)')
plt.ylabel('Cºp,m (J/mol K)')
#Mostra a legenda de cada curva
plt.legend(loc='best')
#mostra o gráfico
plt.show
<function matplotlib.pyplot.show(*args, **kw)>
Em seguida será ajustada a função \(Cº_{p,m} = A + BT + CT^2 + D/T^2 \) aos dados do problema. Neste caso é preciso definir a função segundo a sintaxe do Python e em seguida usar a função curve_fit() para ajustar a função desejada aos dados do problema.
# Definir a função que será ajustada
def func(T, a, b, c, d):
return a + b*T + c*T**2 + d/T**2
# ajuste da função usando mínimos quadrados
# popt são os parâmetros do modelo obtidos após ajuste
# pcov é a matriz de covariância de popt. A partir dela pode ser calculado o desvio padrão de cada parâmetro do ajuste
popt, pcov = curve_fit(func, T, Cp)
print('Cºp,m = ' + format(popt[0] , ' 6.3e') + ' +' + format(popt[1] , ' 6.3e') + 'T ' + format(popt[2] , ' 6.3e') + 'T² +' + format(popt[3] , ' 6.5e') + '/T²')
#imprimir só os coeficientes na forma de vetor
print("Coeficientes da função", popt)
Cºp,m = 2.483e+01 + 1.456e-02T -4.560e-06T² + 4.90797e+04/T²
Coeficientes da função [ 2.48294824e+01 1.45554447e-02 -4.55956846e-06 4.90796782e+04]
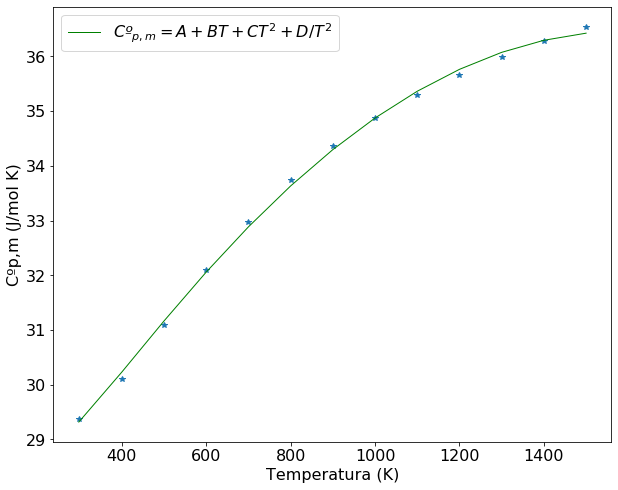
Novamente construiremos o gráfico de Cp versus T com os dados do enunciado e a equação ajustada.É possível perceber que ambas funções se ajustam bem aos dados do problema e que não é possível fazer uso de uma equação de primeiro grau para representar os dados fornecidos. A superposição das curvas confirma a similaridade dos modelos ajustados e que a escolha de uma função ou outra dependerá do problema em questão e das operações matemáticas que serão realizadas posteriormente.
plt.rcParams.update({'font.size': 16}) # estes dois parâmetros precisam aparecer antes da definição do plot
plt.figure(figsize=(10,8))
plt.plot(T,Cp,'*')
#gráfico da função ajustada. O argumento *popt informa que serão usados todos os coeficientes da
# equação que foi ajustada
plt.plot(T,func(T, *popt), color='green', linewidth=1,label='$Cº_{p,m} = A + BT + CT^2 + D/T^2 $')
plt.xlabel('Temperatura (K)')
plt.ylabel('Cºp,m (J/mol K)')
#Mostra a legenda de cada curva
plt.legend(loc='best')
plt.show
<function matplotlib.pyplot.show(*args, **kw)>
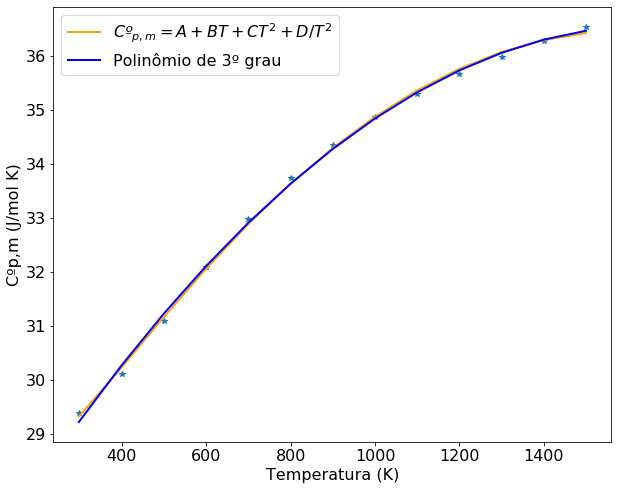
Superposição dos resultados para fins de comparação.
plt.rcParams.update({'font.size': 16}) # estes dois parâmetros precisam aparecer antes da definição do plot
plt.figure(figsize=(10,8))
plt.plot(T,Cp,'*')
plt.plot(T,func(T, *popt), color='orange', linewidth=2, label='$Cº_{p,m} = A + BT + CT^2 + D/T^2 $')
plt.plot(T,y(T), color='blue', linewidth=2, label='Polinômio de 3º grau')
plt.xlabel('Temperatura (K)')
plt.ylabel('Cºp,m (J/mol K)')
#Mostra a legenda de cada curva
plt.legend(loc='best')
plt.show
<function matplotlib.pyplot.show(*args, **kw)>
Exercício 2: Calculando entropias da terceira Lei#
Gráficos de Cp/T versus T são usados para determinar a entropia de um material, uma vez que o valor de entropia é igual a área sob a curva. A tabela abaixo apresenta a variação de Cp do \(Na_2SO_4\) em função da temperatura. a) Ajuste um polinômio de terceira ordem que passa pela origem aos dados fornecidos e calcule a entropia do \(Na_2SO_4\) a 90 K. b) Em baixas temperaturas é possível ajustar uma função do tipo aT³ aos valores de Cp/T (“a” é uma constante). Investigue em qual intervalo de temperaturas esta aproximação é válida. c) Ajuste uma função do tipo \( Cº_{p,m} = A + BT + CT^2 + \frac{D}{T^2} \) e calcule a entropia a 90 K. d) Ajuste uma função do tipo \( Cº_{p,m} = A + BT + CT^2 + DT^3 \) e calcule a entropia a 90 K. Compare os ajustes dos itens (c) e (d).
Cp(\(cal ~ K^{-1}\) ) |
0.171 |
0.286 |
0.626 |
1.615 |
4.346 |
7.032 |
10.48 |
13.28 |
T(K) |
13.74 |
16.25 |
20.43 |
27.73 |
41.11 |
52.72 |
68.15 |
82.96 |
Solução (a)#
Vamos ajustar a função informada no item a e em seguida calcular a entropia resolvendo \( dS = \frac{Cp}{T} dT \) no intervalo de temperaturas informado. Para isto recorremos ao enunciado da terceira lei da termodinâmica:
Para qualquer processo isotérmico que envolve apenas substâncias em equilíbrio interno, a variação da entropia tende a zero à medida que T tende a zero:
Desta forma podemos integrar de 0 K até 90 K, considerando que \(S_0 = 0\) em T = 0 K para \(Na_2 SO_4\). Neste intervalo de temperatura o \(Na_2 SO_4\) se mantém sólido, desta forma não precisamos nos preocupar em levar em consideração as mudanças de fase do sistema.
Os dados do problema serão inseridos na forma de vetores e a função polinomial que cruza a origem será definida segundo a sintaxe do Python. Posteriormente o método dos mínimos quadrados será usado para ajustar a função aos pontos do problema, assim como foi feito no primeiro exemplo.
T = np.array([13.74,16.25,20.43,27.73,41.11,52.72,68.15,82.96,95.71])
Cp = np.array([0.171,0.286,0.626,1.615,4.346,7.032,10.48,13.28,15.33])
# Definir a função que será ajustada
def func(T, b, c, d):
return b*T + c*T**2 + d*T**3
# ajuste da função usando mínimos quadrados
# popt são os parâmetros do modelo obtidos após ajuste
# pcov é a matriz de covariância de popt. A partir dela pode ser calculado o desvio padrão de cada parâmetro do ajuste
popt, pcov = curve_fit(func, T, Cp)
print('Cºp,m = ' + format(popt[0] , ' 6.3e') + 'T +' + format(popt[1] , ' 6.3e') + 'T² ' + format(popt[2] , ' 6.5e') + 'T³')
#imprimir só os coeficientes na forma de vetor
popt
Cºp,m = -5.746e-02T + 5.167e-03T² -3.03363e-05T³
array([-5.74633196e-02, 5.16679456e-03, -3.03363216e-05])
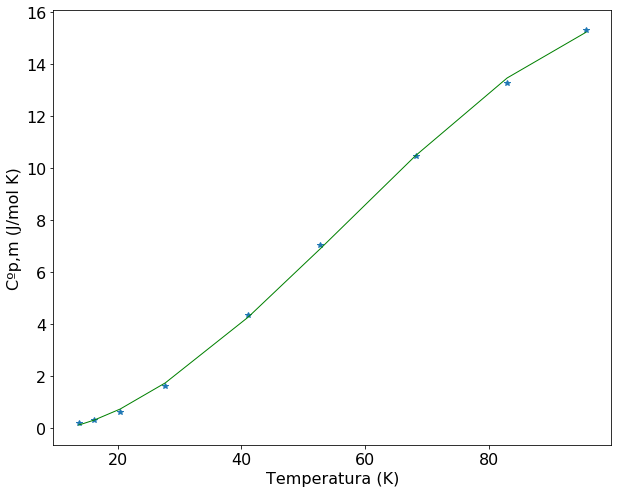
O gráfico do ajuste mais os pontos do problema será construído para verificarmos se a função representa de forma adequada os dados experimentais. Em seguida será definida uma função para o resultado da divisão \(\frac{Cp(T)}{T}\). Esta nova função será integrada de 0 K até 90 K usando a função quad().
plt.rcParams.update({'font.size': 16}) # estes dois parâmetros precisam aparecer antes da definição do plot
plt.figure(figsize=(10,8))
plt.plot(T,Cp,'*')
plt.plot(T,func(T, *popt), color='green', linewidth=1)
plt.xlabel('Temperatura (K)')
plt.ylabel('Cºp,m (J/mol K)')
plt.show
<function matplotlib.pyplot.show(*args, **kw)>
# Fazendo a integração no intervalo desejado
#Definição da função Cp(T)/T
def func(T):
return popt[0] + popt[1]*T + popt[2]*T**2
ans, err = quad(func, 0, 90) #calcula a integral da função da acima e o erro da integração
print('Delta S (J/K mol)= ' + format(ans , '6.3f'))
print('erro da integração = ' + format(err, '6.3e'))
Delta S (J/K mol)= 8.382
erro da integração = 1.006e-13
Solução (b)#
Neste caso é preciso analisar o intervalo no qual o ajusto pedido é válido. Nós faremos um corte nos valores informados na forma de vetores, para criar uma nova lista reduzida de valores. A instrução T[:X], onde X é um número inteiro, faz a retirada dos X primeiros valores do vetor T e os armazena em uma nova variável, chamada de Ti. Em nossa resolução foram considerados os primeiros cinco valores de temperatura. Para que o ajuste possa ser feito, é preciso também extrair os primeiros cinco valores de Cp, caso contrário não será possível proceder com o ajuste de funções a criação de gráficos. O leitor é incentivado a testar outros intervalos e avaliar a variação do desvio padrão calculado e precisão do ajuste. O desvio padrão deste ajuste foi calculado como a raíz quadrada da diagonal da matriz de covariância.
#Corte nos valores iniciais de Cp e T
#Foram tomados apenas os primeiros 5 valores
Ti = T[:5]
Cpi = Cp[:5]
# Definir a função que será ajustada
def func(Ti, a):
return a*Ti**3
a, pcov = curve_fit(func, Ti, Cpi) # faz o ajuste do modelo
perr = np.sqrt(np.diag(pcov)) # calcula o desvio padrão do modelo
#imprimir só os coeficientes na forma de vetor
print('a= ' + format(a[0] , '6.3e'))
print('desvio padrão do ajuste = ' + format(perr[0], '6.3e'))
plt.rcParams.update({'font.size': 16}) # estes dois parâmetros precisam aparecer antes da definição do plot
plt.figure(figsize=(10,8))
plt.plot(Ti,Cpi,'*')
#Gráfico da função
plt.plot(Ti,func(Ti, *a), color='green', linewidth=1, label='$Cp(T)=a^3$')
plt.xlabel('Temperatura (K)')
plt.ylabel('Cºp,m (J/mol K)')
plt.legend(loc='best')
plt.show()
a= 6.383e-05
desvio padrão do ajuste = 1.919e-06
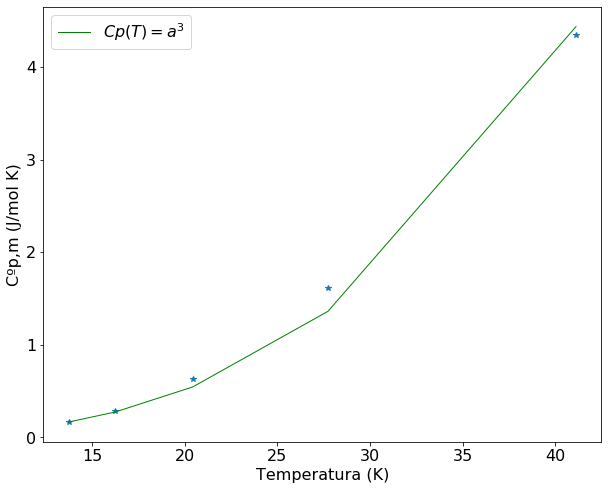
A análise do gráfico e desvio padrão mostra que a função \(aT^3\) se ajusta bem aos primeiros 5 valores de \(C_p\). A equação \(C_p = aT^3\), que define a dependência da capacidade calorífica com a temperatura em valores muito baixos de T, é denominado de Lei de Debye. Esta equação é válida para sólidos não metálicos, pois para sólidos metálicos a temperaturas póximas de 0K é válida a relação \(C_p \sim C_V = aT^3 + bT\).
Solução conjunta dos itens (c) e (d)#
Primeiramente será ajustada a função \( Cº_{p,m} = A + BT + CT^2 + \frac{D}{T^2} \) e calculado \(\Delta S \) em 90 K.O procedimento adotado será o mesmo de exemplos anteriores: 1) definição da função a ser ajustada; 2) ajuste da função por mínimos quadrados; 3) definição da função Cp/T; 4) integração da função Cp/T usando a função quad().
# Considerando a primeira função
# Definir a função que será ajustada
def func(T, a, b, c, d):
return a + b*T + c*T**2 + d/T**2
# ajuste da função usando mínimos quadrados
# popt são os parâmetros do modelo obtidos após ajuste
# pcov é a matriz de covariância de popt. A partir dela pode ser calculado o desvio padrão de cada parâmetro do ajuste
popt, pcov = curve_fit(func, T, Cp)
print('Cºp,m = ' + format(popt[0] , ' 6.3e') + ' +' + format(popt[1] , ' 6.3e') + 'T ' + format(popt[2] , ' 6.3e') + 'T² +' + format(popt[3] , ' 6.5e') + '/T²')
#Definição da função Cp/T
def func(T):
return popt[0]/T + popt[1] + popt[2]*T + popt[3]/T**3
#integração da função Cp/T
ans, err = quad(func, 0, 90)
print('Delta S (J/K mol)= ' + format(ans , '6.3f'))
print('erro da integração = ' + format(err, '6.3e'))
Cºp,m = -6.436e+00 + 2.829e-01T -5.728e-04T² + 5.61810e+02/T²
Delta S (J/K mol)= -36.947
erro da integração = 2.677e+01
<ipython-input-12-900a5a636b92>:24: IntegrationWarning: The integral is probably divergent, or slowly convergent.
ans, err = quad(func, 0, 90)
Perceba que o resultado é muito diferente do obtido no item a e que um aviso foi dado pelo sistema de que a integral é divergente ou tem convergência demorada.
Agora será ajustado um polinômio do terceiro grau e cálculado \(\Delta S\).
# Considerando o polinômio do terceiro grau
deg = 3
z = np.polyfit(T, Cp, deg)
y = np.poly1d(z)
print('Cºp,m = ' + format(z[3] , ' 6.5f') + format(z[2] , ' 6.5f') + 'T + ' + format(z[1] , ' 6.5e') + 'T² ' + format(z[0] , ' 6.5e') + 'T³')
#imprimir só os coeficientes na forma de vetor
print(z)
print()
def func(T):
return y/T # Para simplificar foi usado o polinômio y para definir a função Cp/T
# return z[3]/T + z[2] + z[1]*T + z[0]*T**2 esta seria uma segunda alternativa para definir a função
ans, err = quad(y, 0, 90)
print('Delta S (J/K mol)= ' + format(ans , '6.3f'))
print('erro da integração = ' + format(err, '6.3e'))
Cºp,m = -0.20558-0.04189T + 4.85438e-03T² -2.85176e-05T³
[-2.85176338e-05 4.85438172e-03 -4.18860690e-02 -2.05576078e-01]
Delta S (J/K mol)= 523.714
erro da integração = 5.879e-12
Os três valores de entropia calculados nos itens (a), (c) e (d) diferem quanto ao valor e sinal. Não havendo acordo entre os métodos empregados. Era de se esperar que os três resultados apresentassem uma pequena diferença e não o desacordo observado. O erro ocorre porque as funções utilizadas nos itens (c) e (d) apresentam uma indeterminação na origem, o que levará a problemas de integração. Nestes casos, a integral deve ser separada em dois intervalos:
Como visto no item (b), Cp pode ser ajustado a uma função do tipo \( aT^3\), de forma que a integração se torna:
ou
Onde \(C_p\) da primeira integral da direita se refere ao valor da capacidade calorífica em \(T_{baixa}\). Em nosso caso, é maior valor T para o qual é válido o ajuste da função aT³ usada no item (c). Vamos resolver os problemas com as modificações necessárias.
# Considerando a função Cp = aT^3 em temperaturas baixas
# Não é preciso refazer o ajuste, pois os coeficientes já estão salvos.
#Definição da função Cp/T = aT^3/T
def func1(T):
return a[0]*T**2
ans1, err1 = quad(func1, 0, 40)
def func2(T):
return popt[0]/T + popt[1] + popt[2]*T + popt[3]/T**3
ans2, err2 = quad(func2, 40, 90)
DS = ans1 + ans2
erro = err1 + err2
print('Delta S (J/K mol)= ' + format(DS , '6.3f'))
print('erro da integração = ' + format(erro, '6.3e'))
Delta S (J/K mol)= 8.565
erro da integração = 9.509e-14
# Considerando a função Cp = aT^3 em temperaturas baixas
# Não é preciso refazer o ajuste, pois os coeficientes já estão salvos.
# Esta primeira integração não precisa ser repetida, pois os resultado será o mesmo.
#Mas calcularemos de novo a integral para fixar a necessidade da separação dos cálculos
def func1(T):
return a[0]*T**2
ans1, err1 = quad(func1, 0, 40)
def func2(T):
return z[3]/T + z[2] + z[1]*T + z[0]*T**2
ans2, err2 = quad(func2, 40, 90)
DS = ans1 + ans2
erro = err1 + err2
print('Delta S (J/K mol)= ' + format(DS , '6.3f'))
print('erro da integração = ' + format(erro, '6.3e'))
Delta S (J/K mol)= 8.556
erro da integração = 9.499e-14
Verifiquem que o resultado dos itens (a), (c) e (d) são similares. Novamente, a escolha do modelo matemático dependerá dos cálculos que pretende realizar e as propriedades que pretende calcular.
Sugestão de exercício:#
Resolva os exemplos anteriores usando um método de integração numérica (Regra de Simpson ou do Trapézio) e compare os resultados obtidos com as soluções que fazem uso do polinômio da capacidade calorífica.
