Primeira Lei da Termodinâmica#
Fundamentos teóricos#
Imagine um sistema fechado, por exemplo o refrigerante dentro de uma garrafa ou um cilindro de gás. Este sistema quando em repouso e na ausência de campos externos, apresenta uma determinada energia, denominada energia interna (U). Esta energia está relacionada a energia cinética e potencial das partículas que compõe o sistema. Se desejamos causar alguma alteração no sistema, as únicas maneiras de se fazer isso é esquentando ou resfriando o sistema, ou realizando trabalho.
O primeiro método é intuitivo e pode ser feito por fazer o sistema entrar em contato com um corpo em temperatura mais alta ou mais baixa. Quando isso acontecer, haverá fluxo de calor (Q) do corpo mais quente para o corpo mais frio. Quando o sistema esfriar, significa que este perdeu calor para as vizinhanças, logo sofreu um processo exotérmico (Q < 0). No entanto, quando o sistema esquentar, este recebeu calor das vizinhanças, logo, passou por um processo endotérmico (Q > 0).
No caso do sistema fechado, realizar trabalho significa a princípio provocar uma mudança de volume do sistema contra uma pressão externa. Este trabalho é visto como uma elevação ou abaixamento de uma massa nas vizinhanças. Se houver uma expansão do sistema, elevando uma massa nas vizinhanças, é dito que foi realizado trabalho nas vizinhanças e este é positivo (W > 0). Caso haja uma contração do sistema, é dito que foi realizado trabalho sobre o sistema e este é negativo (W < 0). Matematicamente o trabalho de expansão pode ser definido como:
\(dW = -p_{ex}dV\)
Desta maneira podemos escrever que energia interna de um sistema fechado obedeça a relação:
\(U = Q + W\)
ou na forma diferencial
\(dU = dQ + dW\)
Trabalho e calor são propriedades intrínsecas da transformação que o sistema sofreu, logo, dependem do caminho da transformação. Enquanto que U depende apenas do estado final e inicial do sistema, por isso é chamado de função de estado termodinâmico. Por consequência, em um sistema isolado que passa por uma transformação cíclica
\(dU = 0\)
Os seguintes módulos precisam ser carregados para resolução dos exercícios:
#bibliotecas necessárias para resolução de exercícios
import numpy as np
from scipy.optimize import curve_fit
from scipy.integrate import quad # rotina para integraçã ode funções pelo método da quadratura
import matplotlib.pyplot as plt
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 2
1 #bibliotecas necessárias para resolução de exercícios
----> 2 import numpy as np
3 from scipy.optimize import curve_fit
4 from scipy.integrate import quad # rotina para integraçã ode funções pelo método da quadratura
ModuleNotFoundError: No module named 'numpy'
Exemplo 1: Cálculo do trabalho em uma expansão reversível de um gás ideal#
Considere a compressão reverssível de 1.0 mol de um gás ideal, de 22.4 L para 10.0L mantendo T constante a 0ºC. Calcule o trabalho realizado neste processo. Repita os cáclulos para uma segunda compressão de 10.0 L até 1.0 L mantendo a temperatura a 0ºC.
Solução#
O trabalho reversível é o trabalho teórico máximo que o sistema pode realizar. Este trabalho é teórico pois considera que o trabalho é feito em n etapas infinitesimais. O valor do trabalho dependerá do sistema e da equação de estado que descreve este sistema. Por este motivo, em primeiro lugar é preciso encontrar um expressão para o trabalho p-V de um gás ideal. No trabalho reversível podemos considerar que a pressão de oposição se iguala a pressão do sistema, sendo esta calculada pela equação de estado. Desta forma podemos obter o trabalho reversível de uma gás ideal da seguinte forma:
O problema é dividido em duas etapas. Logo, será calculado o trabalho para primeira compressão, seguido do cálculo do trabalho para segunda compressão. O trabalho total é a soma do trabalho realizado em cada etapa individual.
#Primeira compressão
#Definição das variáveis
R = 8.314 # J/K mol
n = 1.0 # mol
T = 273.15 # K
V1 = 22.4 # L
V2 = 10.0
# Cálculo
W1 = -n*R*T*np.log(V2/V1)
print('W (J/mol)= ' + format(W1 , '6.3f'))
W (J/mol)= 1831.482
# Segunda Compressão
V3 = 1.0 # L
# Cálculo
W2 = -n*R*T*np.log(V3/V2)
print('W (J/mol)= ' + format(W2 , '6.3f'))
W (J/mol)= 5229.100
O trabalho total é a soma dos trabalhos realizados em cada etapa. Neste ponto é ilustrativo comparar o trabalho total realizado em duas etapas, com o trabalho realizado em uma única etapa de 22.4 L até 1 L.
# Trabalho total em 2 etapas
Wtotal = W1 + W2
print('W em duas etapas(J/mol)= ' + format(Wtotal , '6.3f'))
# Trabalho total em uma etapa
W = -n*R*T*np.log(V3/V1)
print('W em uma única etapa (J/mol)= ' + format(W , '6.3f'))
W em duas etapas(J/mol)= 7060.581
W em uma única etapa (J/mol)= 7060.581
Apesar dos resultados serem iguais, o trabalho não é uma função de estado termodinâmico, logo, seu valor não depende apenas do estado final e inicial. A princípio os resultados poderiam ser diferentes.
Exemplo 2: Cálculo do trabalho em uma expansão reversível de um gás de van der Waals#
Repita o exercício anterior para o \(O_2\), assumindo que este se comporta como um gás de van der Waals.
Solução#
Novamente nosso problema se resume a encontrar uma equação com a qual podemos calcular o trabalho feito por um gás de van der Waals.
A equação de estado para um gás de van der Waals é:
Substituindo esta equação na definição do trabalho p-V, encontraremos a expressão desejada.
Assim como no problema anterior será calculado o trabalho para primeira compressão, seguido do cálculo do trabalho para segunda compressão. O trabalho total é a soma do trabalho realizado em cada etapa individual.
#Primeira compressão
#Definiçãodas variáveis
R = 8.314 # J/K mol
n = 1.0 # mol
T = 273.15 # K
V1 = 22.4e-3 # m^3
V2 = 10.0e-3
a = 0.1380 # m^3 Pa / mol^2
b = 0.0319e-3 # m^3 / mol
#Cálculo
W1 = -R*T*np.log((V2-b)/(V1-b)) -a*(1/V2 - 1/V1)
print('W (J/mol)= ' + format(W1 , '6.3f'))
W (J/mol)= 1827.862
# Segunda Compressão
V3 = 1.0e-3 # m^3
W2 = -R*T*np.log((V3-b)/(V2-b)) -a*(1/V3 - 1/V2)
print('W (J/mol)= ' + format(W2 , '6.3f'))
W (J/mol)= 5171.268
Pode-se verificar que o uso da equação de van der Waals leva a resultados distintos aos obtidos com a equação do gás ideal. Para fins didáticos, a comparação anterior do trabalho realizado em em dois estágios com o trabalho em um estágio será refeita.
# Trabalho total em 2 etapas
Wtotal = W1 + W2
print('W em duas etapas(J/mol)= ' + format(Wtotal , '6.3f'))
# Trabalho total em uma etapa
W = -R*T*np.log((V3-b)/(V1-b)) -a*(1/V3 - 1/V1)
print('W em uma única etapa (J/mol)= ' + format(W , '6.3f'))
W em duas etapas(J/mol)= 6999.130
W em uma única etapa (J/mol)= 6999.130
Exemplo 3: Cálculo do trabalho em uma expansão reversível de um gás que obedece uma expansão do virial#
A equação de estado dos gases pode ser escrita na forma de uma expansão do virial, \( pV_m = RT \left( 1 + \frac{B}{V_{m,}} + \frac{C}{V^2_{m}} + ...\right)\). Repita os exercícios anteriores para compressão do \(O_2\) e compare os resultados. Dados: B = \( -22,0 \times 10^{-6} m^3 mol^{-1}\), C = \( 1100 \times 10^{-12} m^6 mol^{-2}\).
Solução#
Em primeiro lugar é preciso encontrar um expressão para o trabalho p-V de um gás que obedece a equação do virial.
Note que o procedimento é o mesmo em todos os casos: Substituir o valor da pressão na equação do trabalho utilizando a equação de estado desejada. Posteriormente resolução da equação diferenção pela integração em ambos os lados. De posse da expressão analítca calcular o trabalho realizado.
#Primeira compressão
#Definição das variáveis
R = 8.314 # J/K mol
n = 1.0 # mol
T = 273.15 # K
V1 = 22.4e-3 # m^3
V2 = 10.0e-3
B = -22.0e-6 # m**3 / mol
C = 1100e-12 # m**6 / mol**2
#Cálculo
W1 = -R*T*(np.log(V2/V1) - B*(1/V2 - 1/V1)-C/2 * (1/V2**2 - 1/V1**2))
print('W (J/mol)= ' + format(W1 , '6.3f'))
W (J/mol)= 1828.726
# Segunda Compressão
V3 = 1.0e-3 # m^3
W2 = -R*T*(np.log(V3/V2) - B*(1/V3 - 1/V2)-C/2 * (1/V3**2 - 1/V2**2))
print('W (J/mol)= ' + format(W2 , '6.3f'))
W (J/mol)= 5185.371
# Trabalho total em 2 etapas
Wtotal = W1 + W2
print('W em duas etapas(J/mol)= ' + format(Wtotal , '6.3f'))
W em duas etapas(J/mol)= 7014.097
Exemplo 4: Cálculo do trabalho em uma expansão reversível de um gás de Redlich-Kwong#
O estado de um gás pode ser descrito pela equação de Redlich-Kwong, \( \left (p +\frac{a}{V_m(V_m +b)T^{1/2}} \right) (V_m - b) = RT \). Repita os exercícios anteriores para compressão do \(O_2\) e compare os resultados. Dados: a = 17,16 \(L^2 K^{1/2} atm. mol^{-2}\), b = \(0,0221 L. mol^{-1}\).
Solução#
Novamente nosso problema se resume a encontrar uma equação com a qual podemos calcular o trabalho feito por um gás que obedece a equação de Redlich-Kwong.
A segunda integral da direita pode ser resolvida pelo método das frações parciais, ou usar diretamente o resultado:
\( \int \frac{1}{x(x+b)} dx = \frac{1}{b} ln \left( \frac{x}{x+b} \right) \)
#Primeira compressão
#Definição das variáveis
R = 8.314 # J/K mol
n = 1.0 # mol
T = 273.15 # K
V1 = 22.4e-3 # m^3
V2 = 10.0e-3
a = 17.16*101.3e-3 # m**6 K^0,5 Pa / mol^2
b = 0.0221e-3 # m**3 / mol
#Cálculo
W1 = -R*T*np.log((V2-b)/(V1-b)) + a/(b*T**0.5) *(np.log(V2/V1) - np.log((V2-b)/(V1-b)))
print('W (J/mol)= ' + format(W1 , '6.3f'))
W (J/mol)= 1840.096
#Cálculo da segunda compressão
V3 = 1.0e-3 # m^3
W2 = -R*T*np.log((V3-b)/(V2-b)) + a/(b*T**0.5) *(np.log(V3/V2) - np.log((V3-b)/(V2-b)))
print('W (J/mol)= ' + format(W2 , '6.3f'))
W (J/mol)= 5370.655
# Trabalho total em 2 etapas
Wtotal = W1 + W2
print('W em duas etapas(J/mol)= ' + format(Wtotal , '6.3f'))
W em duas etapas(J/mol)= 7210.751
A comparação do valor calculado para o trabalho considerando quatro equações de estado distintas mostra que o resultado final depende da equação de estado escolhida. Equações de estado mais complexas que as usadas nestes exercícios são conhecidas e a escolha da equação a ser utilizada dependerá das condições do problema, tipo de transformação que está sendo estudada e a precisão desejada.
Exemplo 5: Cálculo do trabalho associado a uma reação química#
Uma reação química ocorre num vaso de seção reta uniforme de 50 cm², provido de um pistão. Em virtude de reação, o pistão se desloca 15 cm contra a pressão externa de 1 atm. Calcule o trabalho feito pelo sistema.
Solução#
O trabalho é \( W = -\int p_{ext} dV = - p_{ext} \Delta V \), onde a variação do volume é dado pela distância de deslocamento do pistão multiplicado pela área seção reta do mesmo. Perceba que neste caso é usado a pressão externa e não a equaçã ode estado de um gás. É feito desta maneira porque o problema informa que a expansão ocorre contra uma pressão de oposição constante.
# Definindo variáveis
A= 0.0050 #m² (Valor já convertido de cm² para m²)
x = 0.15 #m (Valor já convertido de cm para m)
P = 101325 #Pa (Valor convertido de 1 atm para Pascal)
#Cálculos (Como o pistão se desloca contra a pressão externa, o valor do trabalho será negativo)
Volume = A*x
W= - P*Volume
print("Trabalho (J)=" + format(W,'6.3f'))
Trabalho (J)=-75.994
O trabalho negativo indica que o sistema realizou trabalho sobre as vizinhanças associado a sua expansão.
Exercício 6: Cálculos envolvendo aquecimento de um gás ideal#
Uma amostra de 1,00 mol de um gás ideal monoatômico, Cv = 3/2R, inicialmente a \(p_1\) = 1,00 atm e \(T_1\) = 300 K, é aquecida reversivelmente, até 400 K, a volume constante. Calcule a pressão final, ΔU, Q e W.
Solução#
Para este caso, W = 0, pois V = cte, e dU = dQ. Sabemos que:
Por consequência:
Como Cv é constante, o problema se torna:
#Definindo variáveis
p = 1 #atm
T1 = 300 #K
T2 = 400 #K
R=8.3145 #J K-¹ mol-¹
Cv= 3/2*R
n = 1 #mol
# Primeiro passo - Integração: dU = ∫ Cv*dT
ΔU = Cv*(T2-T1) #Após a integração.
print('ΔU (J/mol) = ' + format(ΔU,'6.2f'))
Q = ΔU
print('Q (J/mol) = ' + format(Q,'6.2f'))
ΔU (J/mol) = 1247.17
Q (J/mol) = 1247.17
Exemplo 7: Cálculos da primeira Lei envolvendo o aquecimento de um gás ideal#
Quando se aquecem 2 mols de \(CO_2\), à pressão constante de 1,25 atm, sua temperatura passa de 250 K a 277 K. A capacidade calorífica molar do \(CO_2\) a pressão constante, \(C_{p,m}\), é 37,11 JK-¹ mol-¹. Calcule Q, ΔH e ΔU.
Solução#
Sabe-se que nessas condições de pressão constante Q = \( \Delta H \). Portanto, temos realizar apenas uma integração:
Como é um gás ideal, \( C_p - C_V = nR \), precisaremos integrar a seguinte equação
Como foi informado \(C_{p,m}\), e o problema se refere a 2 mols de \(CO_2\), o valor de \(C_{p}\) a ser utilizado no problema é 74,22 JK-¹ mol-¹.
#Definindo variáveis
p = 1.25 #atm
T1 = 250 #K
T2 = 270 #K
cp = 74.22 #J K-¹ mol-¹
n = 2 #mol
R = 8.314 # J K-¹ mol-¹
#Cálculo da entalpia
ΔH = n * cp * (T2-T1)
print("ΔH (J) = " + format(ΔH,'6.2f'))
#Cálculo da quantidade de calor
Q = ΔH
print("Q (J) = " + format(Q,'6.2f'))
# Como temos somente o Cp, podemos achar o cv através da relação: nR = Cp - Cv
Cv = cp - n*R
#Cálculo da energia interna
ΔU = n * Cv * (T2 - T1)
print("ΔU (J) = " + format(ΔU,'6.4f'))
ΔH (J) = 2968.80
Q (J) = 2968.80
ΔU (J) = 2303.6800
Exemplo 8: Cálculo da entalpia quando \(C_p\) é função da temperatura#
Qual a variação da entalpia molar do \(N_2\) quando este gás é aquecido de 25°C até 100°C? Considere \(C_{p,m} (J K^{-1} mol^{-1}) = 28,58 + 3,77 \times 10^{-3} T - \frac{0,50 \times 10^5}{T^2}\).
Solução#
Este problema é solucionado resolvendo a seguinte equação:
#Definindo variáveis
T1 = 298 #K
T2 = 373 #K
a = 28.58
b = 3.771e-3 #K-1
c= -0.50e5 #K²
# a, b e c são valores tabelados e que variam de acordo com cada composto estudado
# Escrevendo o resultado analítico da integral:
DeltaH = (a*(T2-T1)) + (1/2*b*(T2**2-T1**2)) - c*((1/T2)-(1/T1))
print(" Diferença de entalpia (J K-¹ mol-¹) =" + format(DeltaH,'6.4e'))
Diferença de entalpia (J K-¹ mol-¹) =2.2047e+03
Exemplo 9: Cálculos envolvendo a capacidade calorífica, quando esta é uma função da temperatura#
A capacidade calorífica a pressão constante de uma amostra de gás ideal varia com a temperatura de acordo com a expressão \(C_p (J ~K^{-1}) = 20,17 + 0,3655 (T/K)\). Calcule Q, W e ΔH, quando a temperatura é elevada de 25°C a 200°C (i) a pressão constante e (ii) a volume constante.
Solução do problema a p = cte#
Sabe-se que nessas condições de pressão constante Q = \( \Delta H \). Portanto, temos que realizar apenas uma integração:
O trabalho é calculado a partir da primeira Lei da Termodinâmica: \( \Delta U = Q + W \). Como é um gás ideal, \( C_p - C_V = nR \), precisaremos integrar a seguinte equação, assumindo 1 mol de gás ideal:
Solução do problema a V = cte#
A volume constante W = 0, logo, o cálculo da entalpia se dará pela seguinte integração :
O calor será calculado a partir da primeira Lei da Termodinâmica: \( \Delta U = Q \). Como é um gás ideal, \( C_p - C_V = nR \), precisaremos integrar a seguinte equação, assumindo 1 mol de gás ideal:
#Definindo variáveis
T2 = 473 #K
T1 = 298 #K
n = 1 #mol
R = 8.3145 #J-¹mol-¹
# (i) = Pressão Constante
# cálculo do calor
Q = (20.17 * (T2 - T1)) + ((0.5*0.3665)*(T2**2-T1**2))
print("a) Q (J) = " + format(Q,'6.2f'))
#Como temos a pressão constante, sabe-se que Q = ΔH. Portanto:
ΔH = Q
print ("a) ΔH (J)= " + format(ΔH,'6.2f'))
# Calculando trabalho:
DeltaU = (20.17-R * (T2 - T1)) + (0.5*0.3665)*(T2**2-T1**2)
W = DeltaU - Q
print("a) W (J) = " + format(W,'6.2f'))
#(ii) Volume Constante
#cálculo da entalpia
ΔH = 20.17 * (T2 - T1) + (0.5*0.3665)*(T2**2-T1**2)
print("b) ΔH (J)= " + format(ΔH,'6.2f'))
# O trabalho depende da variação de volume, portanto:
W1 = 0
print ("b) W (J) = " + format(W1,'6.2f'))
#Calculando o calor.
#Primeiro é obtido a variação da energia interna
DeltaU = (20.17-R * (T2 - T1)) + (0.5*0.3665)*(T2**2-T1**2)
Q = DeltaU
print ("b) Q (J) = " + format(Q,'6.2f'))
a) Q (J) = 28254.76
a) ΔH (J)= 28254.76
a) W (J) = -4964.62
b) ΔH (J)= 28254.76
b) W (J) = 0.00
b) Q (J) = 23290.14
As propriedades termodinâmicas variam de acordo com o tipo de transformação que o sistema sofre. A entalpia só se igual a quantidade de calor quando a transformação é isobárica, em outras situação Q pode diferir do valor de \(\Delta H\). Na ausência de trabalho diferente de expansão, só haverá trabalho se houver variação no volume do sistema.
Exemplo 10: Cálculo da entalpia em diferentes temperaturas#
A entalpia padrão de formação do \(H_2 O(g)\) a 298K é -241,82 kJ/mol. Estime seu valor a 100°C dadas as seguintes capacidades caloríficas molares, a pressão constante: \(H_2 O(g):33,58 ~J K^{-1} mol^{-1}; H_2 (g): 28,84 ~J K^{-1} mol^{-1}; O_2(g): 29,37 ~J K^{-1} mol^{-1}\). Admita que as capacidades caloríficas sejam independentes da temperatura.
Solução#
É possível estimar a variação de entalpia em uma determinada temperatura a partir da entalpia e capacidades caloríficas em uma temperatura de referência. Nestes casos, é aplicada a Lei de Kirchhoff:
Onde \(\Delta C_{p}\) é a diferença das capacidades caloríficas entre produtos e reagentes. A reação de formação da água é:
#Definindo variáveis
T1 = 298 #K
T2 = 373 #K
cpH20 = 33.58 # J K-¹ mol-¹
cpH2 = 28.84 # J K-¹ mol-¹
cpO2 = 29.37 # J K-¹ mol-¹
HH20 = -241820 # J/mol
#Cálculos
#Reação: H2(g) + 1/2* O2(g) ----> H2O (g)
DeltaCp = cpH20 - (cpH2 + (1/2*cpO2))
DeltaH2 = HH20 + DeltaCp*(T2-T1)
print("Entalpia-padrão de formação a 373K (J)=" + format(DeltaH2,'6.2f'))
Entalpia-padrão de formação a 373K (J)=-242565.88
Exemplo 11: Obtenção do polinômio da capacidade calorífica por ajuste polinomial#
Os dados a seguir mostram como a capacidade calorífica molar padrão, a pressão constante, do dióxido de enxofre varia com a temperatura. De quanto aumenta a entalpia molar padrão do \(SO_{2(g)}\) quando a temperatura varia de 298,15 até 1500 K?
T/K |
300 |
500 |
700 |
900 |
1100 |
1300 |
1500 |
\(C_{p,m} (J K^{-1} mol^{-1})\) |
39,909 |
46,490 |
50,829 |
53,407 |
54,993 |
56,033 |
56,759 |
Solução#
Em primeiro lugar é preciso encontrar uma equação que relacione Cp com temperatura, pois esta é função de T no intervalo de valores estudado. A princípio uma regressão polinomial será usada para encontrar a relação entre Cp e T. Em muito dos casos um polinômio de terceiro grau é suficiente para resolver este tipo de problema.
# Escrevendo T e Cp como vetores
T = np.array([300,500,700,900,1100,1300,1500])
cp = np.array([39.909,46.490,50.829,53.407,54.993,56.033,56.759])
#Regressão de um polinômio de terceiro grau
deg = 3
z = np.polyfit(T, cp, deg)
y = np.poly1d(z)
#impressão dos resultados da regressão
print( 'Cp(T)= ' , y)
Cp(T)= 3 2
1.091e-08 x - 4.368e-05 x + 0.06222 x + 24.9
#Construção do gráfico para visualizar a qualidade do ajuste
plt.rcParams.update({'font.size': 16}) # estes dois parâmetros precisam aparecer antes da definição do plot
plt.figure(figsize=(10,8))
plt.plot(T, cp , ".", label = '$C_p$ experimental')
plt.plot(T, y(T), "-", label = 'Polinômio de terceiro grau')
plt.legend(loc='best')
plt.ylabel('Cp (J/K mol)')
plt.xlabel('T (K)')
plt.show()
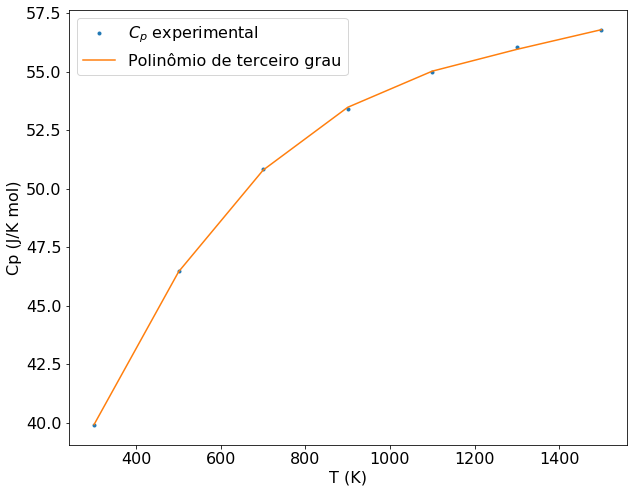
O gráfico confirma que um polinônio de terceiro grau é suficiente para descrever a dependência de \(C_p\) com a temperatura nas condições do problema.A partir do polinômio obtido é possível calcular a variação da entalpia pela integração da capacidade calorífica.
O polinômio foi escrito na ordem em que os coeficientes são guardados no vetor z. A resolução da integral resulta em:
# Realizar a integração da função obtida no intervalo de temperaturas do problema.
# O resultado analítico da integração está escrito abaixo
T2 = 1500 #K
T1 = 298.15 #K
DeltaH = z[0]/4*(T2**4 - T1**4) + z[1]/3*(T2**3-T1**3) + z[2]/2*(T2**2-T1**2) + z[3]*(T2-T1)
print("DeltaH (J)=" + format(DeltaH,'6.2f'))
DeltaH (J)=62199.43
Exemplo 12: Obtendo funções para Cp(T)#
Os dados a seguir mostram como a capacidade calorífica molar padrão a pressão constante da amônia varia com a temperatura. Ajuste uma expressão com a forma \( C_{p,m} = a + bT + \frac{c}{T^2}\) aos dados, e determine os valores de a, b e c. Verifique se não seria melhor expressar os dados na forma \(C_{p,m} = \alpha + \beta T + \gamma T^2\), e determine os valores desses coeficientes.
T/K |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
Cp,m (J K-¹mol-¹) |
35,678 |
38,674 |
41,994 |
45,229 |
48,269 |
51,112 |
53,769 |
56,244 |
Solução#
O ajuste da primeira função será feito usando a rotina scipy.optimize.curve_fit para fazermos uma regressão não linear usando o método dos mínimos quadrados. Inicialmente deve ser definido a função que desejamos ajustar aos dados fornecidos no problema, usando a sintaxe python padrão, e posteriormente proceder com o ajuste. Para comparamos a qualidade de ambos os ajustes, a equação de segundo grau sugerida será ajustada aos dados usando o mesmo procedimento.
#Definindo T e Cp como vetores
T= np.array ([300,400,500,600,700,800,900,1000])
cp = np.array ([35.678,38.674,41.994,45.229,48.269,51.112,53.769,56.244])
# Definir a função que será ajustada usando o formato
# python para descrever funções
def func(T, a, b, c):
return a + b*T + c/T**2
# ajuste da função usando mínimos quadrados
# popt são os parâmetros do modelo obtidos após ajuste
# pcov é a matriz de covariância de popt. A partir dela pode ser calculado o desvio padrão
# de cada parâmetro do ajuste
popt, pcov = curve_fit(func, T, cp)
print('Cºp,m = ' + format(popt[0] , ' 6.3e') + ' +' + format(popt[1] , ' 6.3e') + 'T ' + format(popt[2] , ' 6.5e') + '/T²')
Cºp,m = 2.880e+01 + 2.790e-02T -1.49041e+05/T²
# ajustando um polinômio de segundo grau
# Definir a função que será ajustada usando o formato
# python para descrever funções
def func2(T, a, b, c):
return a + b*T + c*T**2
# ajuste da função usando mínimos quadrados
# popt são os parâmetros do modelo obtidos após ajuste
# pcov é a matriz de covariância de popt. A partir dela pode ser calculado o desvio padrão
# de cada parâmetro do ajuste
popt2, pcov2 = curve_fit(func2, T, cp)
print('Cºp,m = ' + format(popt2[0] , ' 6.3e') + ' +' + format(popt2[1] , ' 6.3e') + 'T ' + format(popt2[2] , ' 6.5e') + 'T²')
Cºp,m = 2.464e+01 + 3.818e-02T -6.49464e-06T²
# Vamos construir os gráficos para ver a diferença nos ajustes
plt.rcParams.update({'font.size': 16}) # estes dois parâmetros precisam aparecer antes da definição do plot
plt.figure(figsize=(10,8))
plt.plot(T, cp , "*") #insere os pontos
plt.plot(T, func(T,*popt), "-", color='blue', linewidth=2, label='Primeiro ajuste') #faz a curva do primeiro ajuste
plt.plot(T,func2(T,*popt2), color='red', linewidth=2, label='Segundo ajuste') #faz a curva do segundo ajuste ajuste
plt.legend(loc='best') #mostra as legendas
#título dos eixos
plt.ylabel('cp (J K-¹mol-¹)')
plt.xlabel('T (K)')
plt.show()
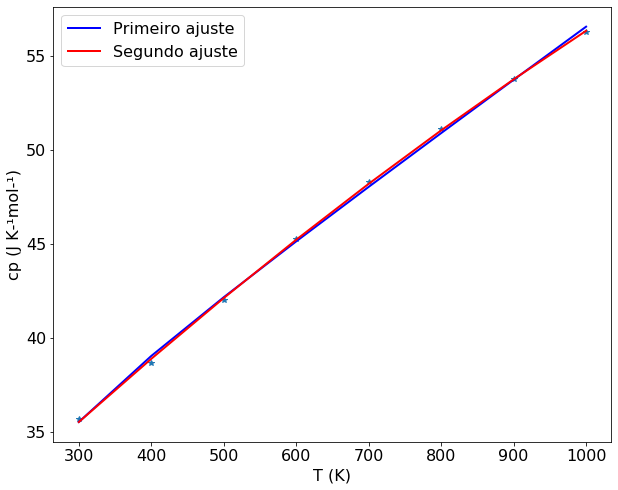
Uma análise visual dos ajustes mostra que ambas as funções são equivalentes. Mas um teste estatístico pode indicar qual das funções se ajusta melhor aos dados experimentais. Como a rotina scipy.optimize.curve_fit retorna a matriz de covariância, é possível calcular o desvio padrão de cada ajuste. Os elementos da diagonal da matriz de covariância fornecem o variância dos parâmetros estimados. A raíz quadrada destes parâmetros fornece o desvio padrão dos parâmetros estimados.
perr = np.sqrt(np.diag(pcov)) # calcula o desvio padrão do primeiro ajuste
perr2 = np.sqrt(np.diag(pcov2)) # calcula o desvio padrão do segundo ajuste
print('desvio padrão do primeiro ajuste = ',perr)
print('desvio padrão do segundo ajuste = ',perr2)
desvio padrão do primeiro ajuste = [8.20143143e-01 9.11188677e-04 6.48021586e+04]
desvio padrão do segundo ajuste = [4.36659308e-01 1.45459699e-03 1.10590957e-06]
Os dois ajustes são distintos, mas analisando o desvio padrão dos dois primeiros coeficientes é possível verificar um menor desvio padrão no ajuste da equação de segundo grau. Logo, seria melhor o uso de uma equação quadrática no lugar da primeira equação.
Exemplo 13: Calculando \( \Delta Hº(T)\) quando Cp é função da temperatura#
Às vezes é mais adequado exprimir a dependência que a capacidade calorífica tem em relação à temperatura pela expressão empírica \(C_{p,m} = \alpha + \beta T + \gamma T^2\). Utilize esta expressão para determinar a entalpia padrão de combustão do metano a 350 K. Use os seguintes dados obtidos a 298 K:
Coeficientes |
\(\alpha (J K^{-1} mol^{-1})\) |
\( \beta (mJ K^{-2} mol^{-1})\) |
\( \gamma (\mu J K^{-3} mol^{-1})\) |
\(CH_{4(g)}\) |
14,16 |
75,5 |
–17,99 |
\(CO_{2 (g)}\) |
26,86 |
6,97 |
-0,82 |
\(O_{2 (g)}\) |
25,72 |
12,98 |
-3,862 |
\(H_2O_{(g)}\) |
30,36 |
9,61 |
1,184 |
Solução#
É possível estimar a variação de entalpia em uma determinada temperatura a partir da entalpia e capacidades caloríficas em uma temperatura de referência. Nestes casos, é aplicada a Lei de Kirchhoff:
Onde \(\Delta C_{p}\) é a diferença das capacidades caloríficas entre produtos e reagentes. Neste caso, devemos calcular inicialmente a entalpia de combustão a 298K a partir de dados tabelados e depois aplicar a Lei de Kirchhoff.
Determinando o ΔH (298):
Os dados de entalpia de formação das espécies individuais podem ser obtidas na literatura:
\( \Delta H_f (CH_44)= -75.0 ~kJ mol^{-1}\)
\( \Delta H_f (O_2)= 0.0 ~kJ mol^{-1}\)
\( \Delta H_f (CO_2)= -394.0 ~kJ mol^{-1}\)
\( \Delta H_f (H_2O)= -286.0 ~kJ mol^{-1}\)
\( \Delta H(298) = ( \Delta H_f(CO_2) + 2\Delta H_f(H_2 O)) - \Delta H_f(CH_4) \)
# Definindo variáveis
T2= 350 #K
T1= 298 #K
#Calculando Delta H a 298K
DeltaH298 = (-394+(-2*286)) - (-75)
print("ΔH(298)=" + format(DeltaH298,'6.1f')+ "kJ/mol")
ΔH(298)=-891.0kJ/mol
Agora será calculado a diferença na capacidade calorífica agrupando os termos de mesma ordem:
\( \Delta \alpha = ( \alpha(CO_2) + 2\alpha (H_2 O)) - \alpha (CH_4) - 2\alpha (O_2)\)
\( \Delta \beta = ( \beta (CO_2) + 2\beta (H_2 O)) - \beta (CH_4) - 2\beta (O_2) \)
\( \Delta \gamma = ( \gamma (CO_2) + 2\gamma (H_2 O)) - \gamma (CH_4) - \gamma (O_2)\)
\( \Delta C_p = \Delta \alpha + \Delta \beta T + \Delta \gamma T^2 \)
A partir do valor de \( \Delta C_p \) é possível obter a variação da entalpia na tempertura desejada.
# Faremos agora a diferença entre os coeficientes
# Para CH4:
a1 = 14.16 # J K-¹mol-¹
b1 = 75.5e-3 # J K-² mol-¹
c1 = -17.99e-6 # J K-³ mol-¹
#Para CO2:
a2 = 26.86 #J K-¹mol-¹
b2 = 6.97e-3 # J K-² mol-¹
c2 = -0.82e-6 # J K-³ mol-¹
#Para O2:
a3 = 25.7 # J K-¹mol-¹
b3 = 12.98e-3 # J K-² mol-¹
c3 = -3.862e-6 # J K-³ mol-¹
#Para H2O:
a4 = 30.36 #J K-¹mol-¹
b4 = 9.61e-3 #J K-¹mol-¹
c4 = 1.184e-6 #J K-¹mol-¹
# ΔCp = Cp produtos - Cp reagentes
# ΔCp = Cp (CO2) + 2Cp (H2O) - {Cp(CH4) + 2Cp (O2)}
Da = 2*a4 + a2 - a1 - 2*a3
Db = 2*b4 + b2 - b1 - 2*b3
Dc = 2*c4 + c2 - c1 - 2*c3
#Integração de ΔCp em função da Temperatura.
# ΔH (350) = ΔHc(298) + [∫ΔCp dT]
# resultado analítico da integração
DH = DeltaH298*1000 + Da*(T2-T1) + Db/2*(T2**2-T1**2) + Da/3*(T2**3-T1**3)
print("Variação de Entalpia em 350 K = " + format(DH/1000,'6.2f') + "kJ/mol")
Variação de Entalpia em 350 K = 119568.61kJ/mol
