Equilíbrio Químico em Misturas de Gases Ideais#
Fundamentos teóricos#
Considere a reação \(aA + bB \rightarrow cC + dD\) que ocorre em fase gasosa. Podemos escrever a energia livre de reação em função do quociente reacional
\(\Delta _r G = \Delta _r Gº -RT lnQ\)
onde \(\Delta _r Gº\) é a energia livre de Gibbs padrão e Q é o chamado quociente reacional. Este pode ser escrito como: \( Q = \frac{p_C ^c p_D ^d}{p_A ^a p_B ^b}\)
No equilíbrio a equação se reduz a \( \Delta Gº = -RT ~ lnK \), onde \(K\) é a constante de equilíbrio da reação e é expressa da mesma maneira que o quociente reacional. No entanto, são usadas as pressões parciais de equilíbrio para o cálculo de \(K\). Esta constante pode ser escrita em função das frações molares e concentrações molares da seguinte forma:
\(K = K_x p^{\Delta \nu}\) onde \(K_x = \frac{x_C ^c x_D ^d}{x_A ^a x_B ^b}\).
\(K = K_c (RT)^{\Delta \nu}\) onde \(K_c = \frac{[C] ^c [D] ^d}{[A] ^a [B] ^b}\).
A constante de equilíbrio depende de T segundo a equação de van’t Hoff:
\( \frac{\partial lnK}{\partial 1/T} = \frac{\Delta_r Hº}{R T^2} \)
Se assumirmos que \(\Delta_r Hº\) é independente da temperatura, a equação diferencial pode ser resolvida resultando em:
\( ln \frac{K_2}{K_1} = -\frac{\Delta_r Hº}{R} \left (\frac{1}{T_2} – \frac{1}{T_1} \right )\)
No equilíbrio \(\Delta _r Gº \) é um mínimo em termos da composição que pode ser expresso como:
onde \(\xi \) é o grau de avanço da reação e está associado a composição de equilíbrio. Por este motivo é possível encontrar a composição de equilíbrio minimizando \(\Delta _r G \).
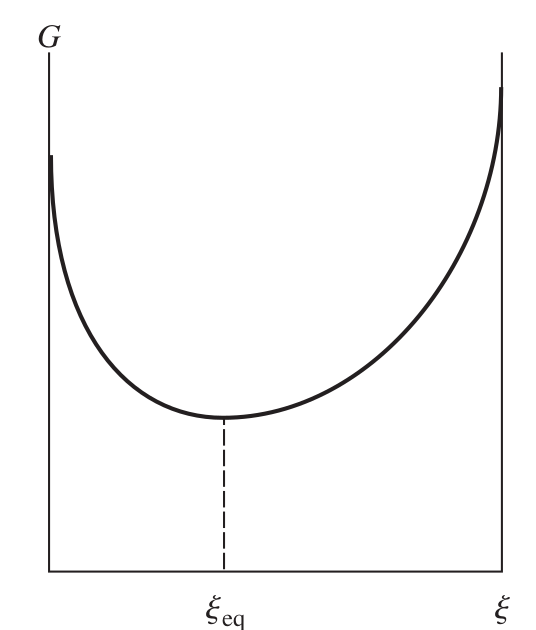
Extraído de [Levine, 2009]
Para a resolução dos exercíos faremos uso das bibliotecas Numpy e Matplolib.
#módulos para resolução dos exercícios:
import numpy as np
from scipy.optimize import fsolve
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 2
1 #módulos para resolução dos exercícios:
----> 2 import numpy as np
3 from scipy.optimize import fsolve
ModuleNotFoundError: No module named 'numpy'
Exemplo 1: Cálculo da constante de equilíbrio e composição de equilíbrio#
a) Use tabelas de dados termodinâmicos para calcular a constante de equilíbrio da reação \( N_2(g) + O_2(g) \rightarrow 2NO(g) \) em T = 298.15 K e 1 bar (0.987 atm). Calcule a concentração de equilíbrio de NO no ar atmosférico em b) T = 298.15 K e 1 atm e c) T = 2000 K e 1 atm.
Solução:#
Em primeiro lugar deve ser calculado a energia livre de reação. Em seguida a relação \( K = -RTln(\Delta_r G^0)\) será usada para o cálculo da constante de equilíbrio a 298K. Para este tipo de reação, a expressão da constante de equilíbrio em termos das pressões parciais é igual a constante em termos de frações molares. Assim podemos assumir a composição aproximada do ar como \(N_2\) = 0.78 e \(O_2\) = 0.21 e que devido a magnitude da constante de equilíbrio estes valores não se alteram apreciavelmente. Será usada a relação \( K = K_x \times p^{\Delta \nu}\) para resolver o exercício.
Por último usamos a equação \( ln(\frac{K_2}{K_1}) = -\frac{\Delta H^0}{R} \times (\frac{1}{T_2}-\frac{1}{T_1}) \) para obter a constante a 2000 K e estimar a concentração de equilíbrio de NO.
#Definição das variáveis:
T = 298.15 #[K] temperatura
P = 0.987 #[atm] pressão
R = 8.314 #[J/(mol*K)]
g_0_NO = 86.6 #[kJ/mol] G padrão de formação do NO
g_0_O2 = 0.00 #[kJ/mol] G padrão de formação do O2
g_0_N2 = 0.00 #[kJ/mol] G padrão de formação do N2
# cálculo do DeltaG
delta_g_0 = 2*g_0_NO - g_0_O2 - g_0_N2 #[kJ/mol]
delta_g_01 = delta_g_0*1000 #[J/mol]
# Cálculo de K
K_298 = np.exp((-delta_g_01)/(R*T))
#composição do ar atmosférico
y_N2 = 0.78
y_O2 = 0.21
y_NO_298 = np.sqrt(K_298*y_N2*y_O2)
print( " Constante de equilíbrio a 298.15 K é \t\t\t %.1e"%(K_298))
print(" A fração molar de NO no equilíbrio a 298K é \t\t %.1e"%(y_NO_298))
Constante de equilíbrio a 298.15 K é 4.5e-31
A fração molar de NO no equilíbrio a 298K é 2.7e-16
De acordo com o resultado, na atmosfera não poluída a 298 K, a concentração de NO é negligenciável. Agora será usada a equaçã ode van’t Hoff integrada para obtermos a constante de equilíbrio a 2000 K e recalcularmos a nova concentração de equilíbrio do NO.
A reação estudada é exatamente a reação de formação do NO. Logo, a entalpia usada na equaçã ode van’t Hoff será \(\Delta Hº _f (NO) \).
#item (c)
T_1 = 2000 #[K]
h_0_NO = 90.25 # kJ/mol H padrão de formação do NO
#cálculo K
K_2000 = np.exp(np.log(K_298) -2*h_0_NO*1000/R *(1/T_1 -1/T))
y_NO_2000 = np.sqrt(K_2000*y_N2*y_O2)
print( " Constante de equilíbrio a 2000 K é \t\t\t %.1e"%(K_2000))
print( " A fração molar de NO no equilíbrio a 2000 K é \t\t %.1e "%(y_NO_2000))
Constante de equilíbrio a 2000 K é 3.7e-04
A fração molar de NO no equilíbrio a 2000 K é 7.8e-03
O aumento da temperatura levou ao aumento da constante de equilíbrio e formação de NO. Neste caso o aumento da temperatura leva a um aumento do rendimento da reação.
Exemplo 2: Cálculo da composição de equilíbrio#
Refaça o cálculo da concentração de equilíbrio NO, do exercício anterior, a 2000 K e 1 atm, mas desta vez sem negligenciar a variação na concentração de \(O_2\) e \(N_2\).
Solução#
A solução tradicional é montar o quadro que expressa o equilíbrio químico e resolver a equação quadrática resultante. Uma alternativa, que será usada neste exemplo, é a minimização da energia livre de Gibbs de reação a partir das equações que descrevem o modelo. Sabemos que \(\Delta G_r º\) é um mínimo no equilíbrio, logo, a derivada primeira em função do grau de avanço da reação deve ser igual a zero. Nesta condição obtemos a composição da mistura reacional.
A solução do problema começa por escrever o quadro que representa o equilíbrio da reação:
\(O_2\) |
\(N_2\) |
2NO |
|
ini |
0.21 |
0.78 |
0 |
eq |
0.21-x |
0.78-x |
2x |
A composição de equilíbrio será substituída na equação da constante de equilíbrio:
Este exemplo abaixo mostrará como utilizar a biblioteca fsolv para resolver problemas de equilíbrio químico. Para isso é preciso que a função seja escrita de forma que sejam calculadas suas raízes. Neste caso:
A sintaxe para resolver o problema é: x = fsolv(função, chute inicial) Como será calculado a fração molar, x deve ser < 1.
Temp = 2000. #[K]
K_2000 = 3.7e-4
#escrevendo uma função no formato do python para cálculo do mínimo da energia livre
# a função fsolve vai encontrar as raízes de uma função. Pode ser utilizada para resolução de sistemas.
def f(x):
return (2*x)**2 - K_2000*(0.78-x)*(0.21-x)
x = fsolve(f,0.01) # encontrar o valor de x que zera a função
c_NO = 2*x
print(" Fração molar do NO calculado neste exemplo %.1e"%(c_NO))
Fração molar do NO calculado neste exemplo 7.7e-03
Exemplo 3#
Determine a composição de equilíbrio para isomerisação do isobutano:
butano <=> isobutano K = 4.52
Pra resolver o exercício basta escrever a constante de equilíbrio em termos da fração molar de isobutano
Depois usamos o fsolve para minimizar a energia de Gibbs, assim com ofoi feito no exemplo anterior.
K = 4.52
def f(x_iso):
return x_iso/(1-x_iso)-K
x_iso = fsolve(f,0)
print(" Fração molar do isobutano %0.2f"%(x_iso))
Fração molar do isobutano 0.82
Exemplo 4#
Plantas modernas para produção de amônia trabalham em torno de 400ºC e 150 atm de pressão. Considerando estas condições, estime a conversão no equilíbrio. Assuma comportamento de gás ideal. K(400ºC, 1 bar) = 0.0137
Solução#
A reação em questão é \( 0.5N_2(g) + 1.5H_2(g) \rightarrow NH_3(g) \). Inicialmente deve-se montar o quadro de equlíbrio e substituir as frações na equação da constante de equilíbrio
0.5\(N_2\) |
1.5\(H_2\) |
\(NH_3\) |
||
ini |
0.5 |
1.5 |
0 |
|
eq |
0.5-0.5x |
1.5-1.5x |
x |
|
x |
\( \frac{0.5-0.5x}{2.0-x}\) |
\( \frac{1.5-1.5x}{2.0-x}\) |
\( \frac{x}{2.0-x } \) |
\( K_x = \frac{\frac{x}{2.0-x}}{(\frac{0.5-0.5x}{2.0-x})^{0.5} \times (\frac{1.5-1.5x}{2.0-x})^{1.5}} \)
Como foi fornecido a constante a 1 bar, é preciso recalcular o valor da constante de equilíbrio a 150 atm. Lembre-se que \(K_p\) é independente da pressão.
\(K_{400°C,1bar} = K_{x} \times p^{\Delta \nu_i} = K_{x} \times p[bar]^{(1-0.5-1.5)}\)
\(K_{400°C,1bar} = K_{x} \times p[bar]^{-1}\)
Temp = 273.15+400 #[K]
P = 150*1.01325 #[bar]
K_673 = 0.013
#calculando a constante a 150 atm
K = K_673*P**(1.5+0.5-1)
#escrevendo a função que descreve o problema de equilíbrio
def f(x):
return (x/(2-x))/(((0.5-0.5*x)/(2-x))**(0.5)*((1.5-1.5*x)/(2-x))**(1.5))-K
x=fsolve(f,0.1)
y_NH3 = x/(2-x)
print("A fração molar de amônia no equilíbrio é %0.2f"%(y_NH3))
A fração molar de amônia no equilíbrio é 0.31
Ira Levine. Physical Chemistry. McGraw-Hill, 2009.
