Energia Livre#
Fundamentos Teóricos#
A espontaneidade de um processo químico pode ser avaliado pela variação na energia livre de Gibbs, $\Delta G$. Esta função de estado termodinâmica é definida como:Onde:
G < 0: processo espontâneo
G > 0: processo não espontâneo
G = 0: equilíbrio
Podemos escrever a equação fundamental da energia livre da seguinte forma:
Sendo \( G = G(T,p) \), indicando que T e p são variáveis naturais de G, isto é, variáveis que podem ser controladas nas vizinhanças do sistema e que afetarão o valor de G. Um processo que ocorre em um sistema a T e p constante estará em equilíbrio quando a energia livre de Gibbs for um mínimo. Como consequência da equação fundamental, em um sistema com composição constante:
\(-S = \left ( \frac{\partial G}{\partial T} \right)_p \), \(V = \left ( \frac{\partial G}{\partial p} \right)_T\)
#bibliotecas necessárias para resolução de exercícios
import numpy as np
from scipy.integrate import simps
import matplotlib.pyplot as plt
#from matplotlib import cm
#from matplotlib.ticker import LinearLocator
from mpl_toolkits.mplot3d import Axes3D
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 2
1 #bibliotecas necessárias para resolução de exercícios
----> 2 import numpy as np
3 from scipy.integrate import simps
4 import matplotlib.pyplot as plt
ModuleNotFoundError: No module named 'numpy'
Exemplo 1: Cálculo de G durante uma expansão#
Determine \(\Delta G\) para compressão de 1,00 mol de uma amostra de \(O_2\) a 0ºC, de 1,00 bar até o 10,0 bar a partir dos seguintes dados de p-V:
p(bar) |
1,000 |
1,500 |
2,000 |
3,000 |
4,000 |
6,000 |
8,000 |
10,00 |
\(V_m\)(L/mol) |
27,711 |
15,133 |
11,344 |
7,555 |
5,661 |
3,767 |
2,820 |
2,251 |
Solução#
A dependência de G com a pressão é dado pela seguinte relação: \( \left ( \frac{\partial G_m}{\partial p} \right )_T = V_m \)
A resolução desta equação diferencial por separação de variáveis leva a integral:
Logo, o valor de \( \Delta G_m \) é a área abaixo da curva p-V, que pode ser calculado por algum método de integração numérica.
p = np.array([1.000,1.500,2.000,3.000,4.000,6.000,8.000,10.00])*1e5 #Pa
V = np.array([27.711,15.133,11.344,7.555,5.661,3.767,2.820,2.251])*1e-3 #m³/mol
G = simps(p, V) # integração usando a regra de Simpson
print('\u0394G (J/mol) = ' + format(G, '6.3e'))
ΔG (J/mol) = -5.785e+03
Exemplo 2#
Foram obtidas as seguntes equações para \(G_m, S_m\) e \(V_m \):
a) Contrua gráficos para \(G_m, S_m ~e~ V_m \) no intervalo de 100 a 500 K e 0,1 a 20 bar. Discuta a inclinação dos gráficos em termos de T e p.
Solução#
A construção dos gráficos seguirá os seguintes passos:Definição do intervalo de T e p na forma de vetor;
Definição das funções que descrevem as propriedades termodinâmicas;
Construção da superfície usando plt.axes(projection=’3d’) e ax.plot_surface(…)
#Definição do intervalo de valores de T e p
T = np.linspace(100,500,100)
p = np.linspace(0.1,20,100)
#definição das funções termodinâmicas
def G(T,p):
return -T * np.log(T**2.5/p)
def S(T,p):
return np.log(T**2.5/p)
def V(T,p):
return T/p
# transforma os vetores em uma matriz
X, Y = np.meshgrid(T, p)
#calcula o valor das propriedades termodinâmicas de acordo com o grid gerado
Z1 = G(X,Y)
Z2 = S(X,Y)
Z3 = V(X,Y)
plt.rcParams.update({'font.size': 12}) # estes dois parâmetros precisam aparecer antes da definição do plot
fig = plt.figure(figsize=(12,8)) # as 2 linhas controlam o tamanho do gráfico
#cria a superfície desejada
ax = plt.axes(projection='3d')
surf = ax.plot_surface(X, Y, Z1, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
#ax.set_title('surface');
ax.set_xlabel('T (K)', labelpad=20)
ax.set_ylabel('p (bar)', labelpad=20)
ax.set_zlabel('G', labelpad=20)
#adiciona uma escala de cores
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
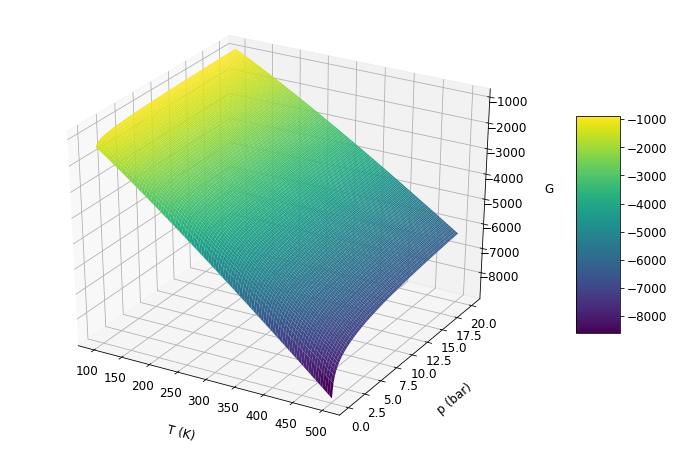
De acordo com o gráfico, o aumnto da temperatura e diminui a energia de Gibbs, enquanto que o aumento da pressão leva ao aumento de G. Logo, G é diretamente proporcional e pressão e inversamente proporcional a temperatura.
Agora é só repetir a construção do gráfico apra as outras propriedades termodinâmicas.
plt.rcParams.update({'font.size': 12}) # estes dois parâmetros precisam aparecer antes da definição do plot
fig = plt.figure(figsize=(12,8))
ax = plt.axes(projection='3d')
surf = ax.plot_surface(X, Y, Z2, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
#ax.set_title('surface');
ax.set_xlabel('T (K)', labelpad=20)
ax.set_ylabel('p (bar)', labelpad=20)
ax.set_zlabel('S', labelpad=20)
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
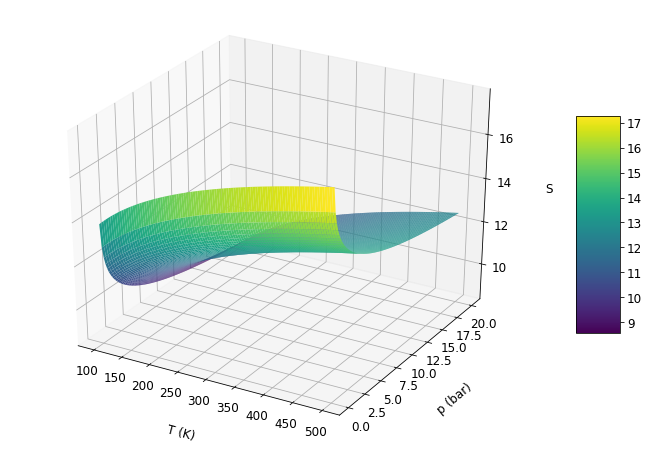
A entropia apresenta um mínimo quando T e p variam simultaneamente. O abaixamento da pressão e aumento da temperatura levam ao aumento da entropia. Logo, a entropia é diretamente proporcional a T e inversamente proporcional p.
plt.rcParams.update({'font.size': 12}) # estes dois parâmetros precisam aparecer antes da definição do plot
fig = plt.figure(figsize=(12,8))
ax = plt.axes(projection='3d')
surf = ax.plot_surface(X, Y, Z3, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
#ax.set_title('surface');
ax.set_xlabel('T (K)', labelpad=20)
ax.set_ylabel('p (bar)', labelpad=20)
ax.set_zlabel('V', labelpad=20)
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
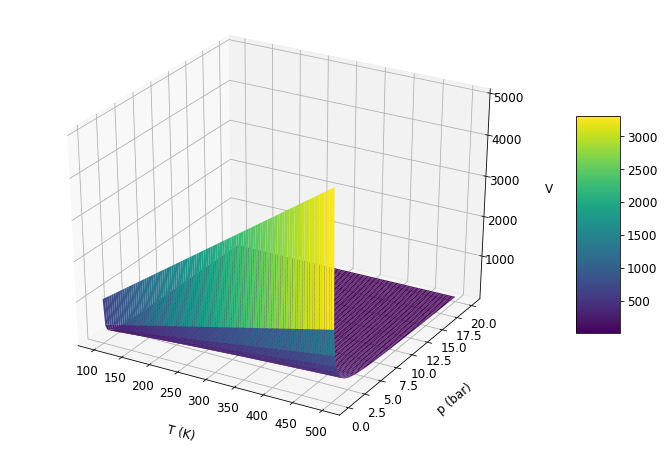
Este gráfico confirma as leis empríricas dos gases: V é inversamente proporcional a p e diretamente proporcional a temperatura.
Exemplo 3: Calculando entropia#
Use os dados da tabela para calcular $ \frac{G^0 _T - H^0 _{298K}}{T}$ para o $CCl_4$ a 1425 K.T(K) |
1000 |
1200 |
1400 |
1600 |
1800 |
2000 |
\( \frac{G^0 _T - H^0 _{298K}}{T}\)(J/K mol) |
-357,595 |
-370,798 |
-382,757 |
-393,632 |
-403,577 |
-412,725 |
Solução#
Pela definição de G, pode-se observar que a grandeza que está sendo calculada é a entropia a 1425 K. O cálculo é feito assumindo que a entalpia é constante em todo o intervalo de temperaturas. O problema pode ser resolvido de duas formas:Verificando que \( \frac{G^0 _T - H^0 _{298K}}{T} \) tem uma dependência quase linear com T, e depois fazer uma interpolação linear para obter o valor desejado;
Ajustar um polinômio aos dados do problema e, de posse da equação, calcular o valor da entropia na temperatura desejada.
Solução 1:#
Será usada a biblioteca numpy.interp((x, xp, fp) para fazer a interpolação linear. Os argumentos da função são:
x: A temperatura em que se deseja fazer o cáclulo
xp: A variável independente, neste caso, T
fp: A variável dependente
Inicialmente o gráfico será cosntruído para verificar a dependência linear dos pontos com a temperatura.
T = np.array([1000,1200,1400,1600,1800,2000])
S = np.array([-357.595,-370.798,-382.757,-393.632,-403.577,-412.725])
# Criando os gráficos
# estes dois parâmetros precisam aparecer antes da definição do plot
plt.rcParams.update({'font.size': 16}) #define o tamanho da fonte
plt.figure(figsize=(10,8)) #define as dimensões do gráfico
plt.plot(T,S, '-*', color='blue', linewidth=1)
plt.xlabel('T (K} ')
plt.ylabel(r'$ \frac{G^0 _T - H^0 _{298K}}{T}$')
plt.show
<function matplotlib.pyplot.show(*args, **kw)>
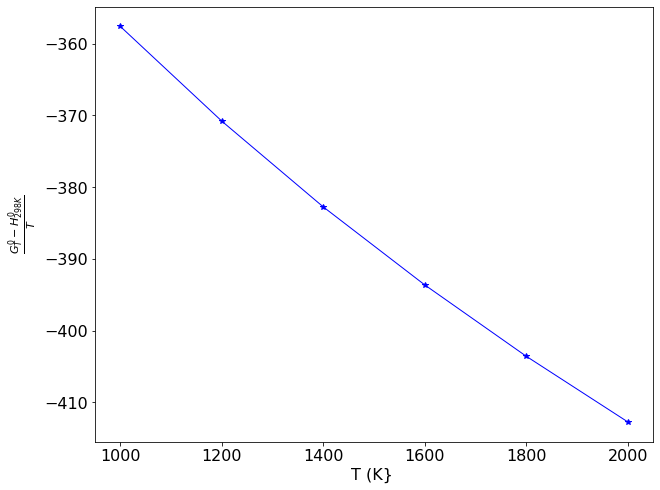
De acordo com o gráfico, a função \( \frac{G^0 _T - H^0 _{298K}}{T}\) é inversamente proporcional a T, e decresce quase que linearmente a medida que T aumenta. Logo, a interpolação linear entre 2 pontos é suficiente para obter o valor desejado.
# Interpolação
s = np.interp(1425, T, S)
print('Entropia a 1425K (J/K mol)= ', s)
Entropia a 1425K (J/K mol)= -384.116375
Solução 2:#
Fazer a regressão e substituir o valor da temperatura na equação obtida. O gráfico apresenta uma leve curvatura a medida que T aumenta, logo, uma função de segundo grau deve se ajustar de forma adequada ao pontos do problema.
#ajuste do polinômio
deg = 2
z = np.polyfit(T, S, deg)
y = np.poly1d(z)
print('Entropia a 1425K (J/K mol)= ', y(1425))
Entropia a 1425K (J/K mol)= -384.12824112723223
Como esperado os resultados são similares mas diferentes. Isso é esperado porque os procedimentos adotados para o cálculo são diferentes. O leitor é encorajado a verificar o resultado usando uma função de primeiro grau. Neste caso a diferença entre os dois resultados será maior, pois a função de primeiro grau não se ajusta tão bem aos dados fornecidos no problema. Isso mostra a importância de de uma verificação prévia dos dados antes de qualquer cálculo.
